用割圓術計算圓周率會遇到計算上的極大困難。
阿基米德從圓的內接和外切正六邊形開始計算,然后把邊數加倍到12邊、24邊、48邊,最后直至96邊。他證明了“圓周率小于3又7分之1而大于3又71分之10”。這表明精確到兩位小數的值就是π≈3.14.
弗蘭西斯·韋達(1540~1603)于1579年用6×2¹?=393216邊的正多邊形求出π精確到9位小數的值。魯道夫·范·休倫(1540~1610)用2?²邊的多邊形計算π精確到35位小數的值。據說這個計算耗費了他幾乎一生時光。
不幸的是,以上計算過程中的每一次新的近似都需要求一個新的平方根。
阿基米德的五重平方根得到兩位小數的精度,更糟糕的是韋達所求的17重平方根只得到9位小數的精度。而令人望而生畏的是魯道夫需要手工計算五打的嵌套平方根,而且每次計算都需要取35位小數。歐拉(1707~1783)將這種工作比喻為大力神海格力斯式的笨重勞動。
所幸的是還有其他計算方法。英國數學家詹姆斯·格雷戈里發現的反正切函數的無窮級數:
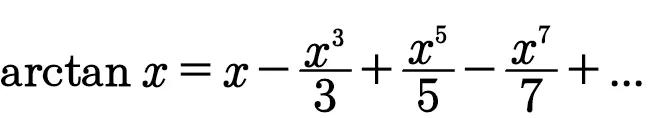
反正切級數
對于x=1,得到萊布尼茨級數¼π=arctan(1)=1-(1/3)+(1/5)-(1/7)+(1/9)-...
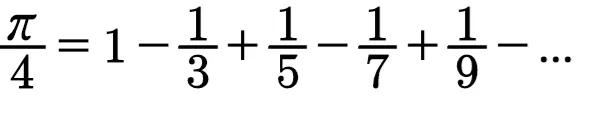
萊布尼茨級數
雖然萊布尼茨級數優雅和簡潔,但是在計算圓周率方面沒有實用價值,因為它的收斂速度太慢了。
然而,如果我們代入一個接近于零的x值,收斂速度就會加快。例如,令x=√3的倒數,得到
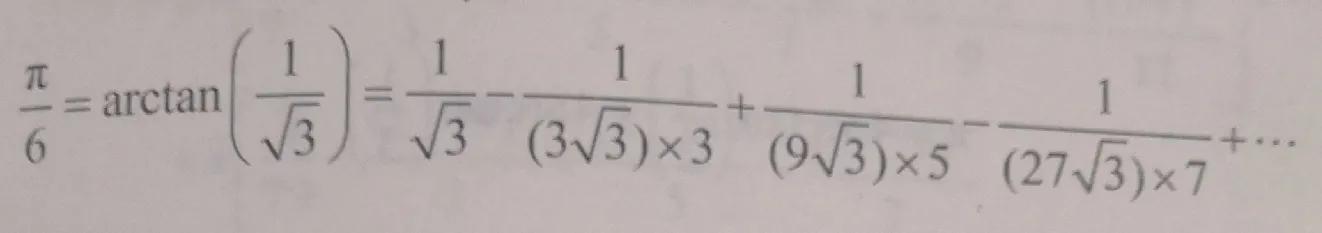
所以
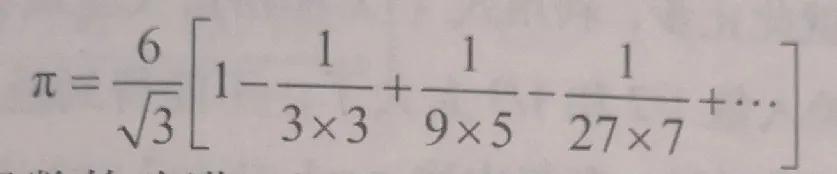
這是對萊布尼茨級數的改進,因為各項的分母增長非常快。另一方面,1/√3≈0.577并不是那么小,而且這個級數包含平方根,這本身就需要取近似值。
對于一位18世紀的數學家來說,理想的計算公式就是使用格雷戈里無窮級數,取充分接近于零的 x 值,同時避免求平方根。這在歐拉1779年的一篇論文中有明確的描述。他的關鍵發現是
π=20arctan(1/7)+8arctan(3/79) (5)
初看起來像是一個印刷錯誤。盡管似乎是不可能的,但是,這是一個等式而不是估值。下面是歐拉對它的證明。
他從恒等式
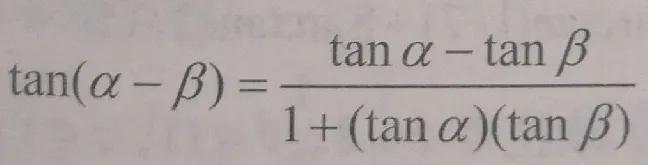
tan (α-β)正切差角公式入手,將其改寫成α-β=
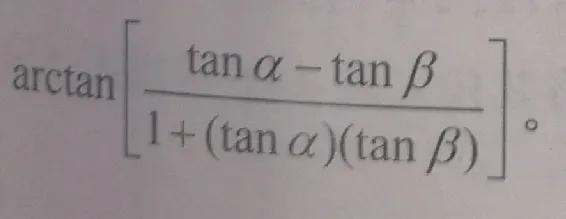
歐拉令 tan α=x /y,tanβ=z/w,得到
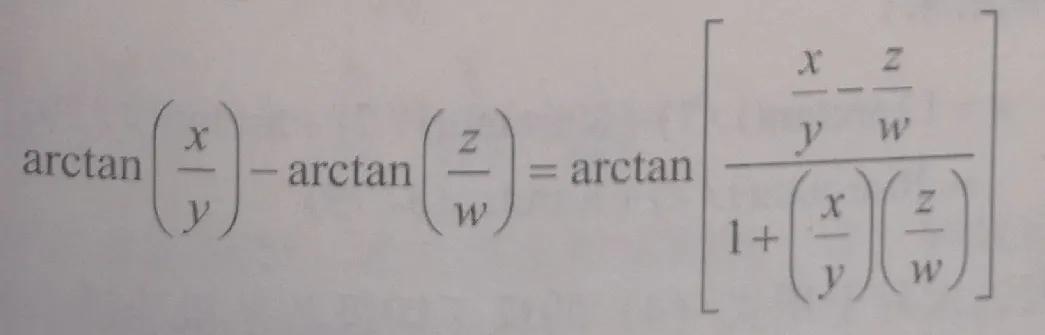
或化簡為